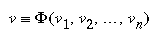
A definition of an object is expressed as a mathematical expression. A variable is called a formula variable if its value is defined in terms of other variables, e.g:
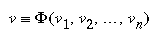
where v is the name of the formula variable, and
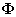 represents an expression with the variables
v1, v2,
... , vn involved. The variables
v1, v2, ...
, vn are called the source variables of this
definition since the value of v is computed from their
values. Hence the formula variable v, can also be called the target
variable. EDEN supports the concept of definition. A formula definition
has the form:
represents an expression with the variables
v1, v2,
... , vn involved. The variables
v1, v2, ...
, vn are called the source variables of this
definition since the value of v is computed from their
values. Hence the formula variable v, can also be called the target
variable. EDEN supports the concept of definition. A formula definition
has the form:
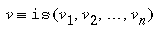
The keyword ``is'' defines a formula variable v whose value
is computed from the values of source variables
v1, v2, ...,
vn and the expression on the right hand
side, denoted by 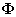 , is the formula of the
variable . In other words, a formula describes how the
value of a variable is computed from other data. These formulae are
permanently valid (unless they are re-defined). That is, no matter
what the values of source variables are, the value of variable
is always equal to
, is the formula of the
variable . In other words, a formula describes how the
value of a variable is computed from other data. These formulae are
permanently valid (unless they are re-defined). That is, no matter
what the values of source variables are, the value of variable
is always equal to  . Thus a formula gives an abstract definition of a
variable rather than the explicit value of it. This is the major
difference between formula definitions and assignment statements. For
example, after executing the assignment
. Thus a formula gives an abstract definition of a
variable rather than the explicit value of it. This is the major
difference between formula definitions and assignment statements. For
example, after executing the assignment
v is equal to  only after the expression
only after the expression 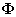 is evaluated
and before any of the values of the source variables is altered.
is evaluated
and before any of the values of the source variables is altered.
Unlike the assignment statement, the formula definition, itself, is not an executable statement. When and how the formula expression defined in the definition is managed by the system. However, the values of the formula variables are guaranteed to be up-to-date when the variables are examined.
Notice that a definition does not imply the inverse definitions (where these exist); for example, the definition (2-1) does not imply
 where 1<=i<=n
where 1<=i<=n
A definition can be a representation of a real relationship among objects; for instance, ``a lamp is placed (somewhere) on a table'' can be formulated as:
lamp_position is table_position + something
If the table is re-positioned the lamp will also be moved because the
definition has specified the position of the lamp in terms of the position
of the table, the system can automatically keep track of these definitions
and re-calculate lamp_position whenever table_position has been changed.
But if the lamp_position is then redefined to
lamp_position is desk_position + something
we mean to put the lamp on the desk instead of the table. The table remains
at the same position because it is not defined in terms of the lamp. Note
that the new definition of lamp_position overwrites the previous definition.
Hence the lamp can be moved independently by redefining its definition.