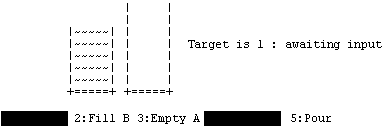
Figure 5.1: A Sample Jugs Output
T5.2.1. Visualisation in Program Design: The Jugs Program revisited
Designing orthodox sequential programs using definitive scripts is a first step towards concurrent systems modelling. Significantly, in generalising single-agent definitive programming, traditional sequential programming is a not particularly natural special case. This is illustrated by the fact that there is no particular reason why we should not redesign the speedometer display in the VCCS whilst the simulation is in use. Conventions by which agents are restricted to exercise privileges according to a specified pattern are inappropriate in the first stage of specification; they only serve to obscure the experimental foundation for behaviour. A similar philosophy lies behind concepts such as Jackson System Development, where the designer is encouraged to model the application domain prior to developing the application. In this section, we illustrate how single-agent definitive programming can be applied to developing a simple program that is eventually to be used in a sequential mode. Simon Yung designed and implemented Scout, and the analysis and commentary that follows is taken from his doctoral thesis: Definitive Programming as a Paradigm for Exploratory Software Development.
Jugs is a simple simulation program originally developed by Townsend,
that was first considered from a DST perspective in [BNRSYY89]. There are
two jugs, A and B, with different capacities, capA and capB respectively.
capA and capB should be relatively prime. One can choose an operation from
a set of permissible menus at a time. The whole range of operations is:
2) fill Jug B,
3) empty Jug A,
4) empty Jug B, and
5) pour as much water from Jug A to Jug B or from Jug B to Jug A as
the destination jug can hold.
The program designer's task is to develop a script in which the roles of a user of the jugs program and of the computer simulation of operations on the jugs can be specified. (The distinction between a pupil user, who selects menu options, and a teacher user, who can set up problems for the pupil is also of interest.) The programming principles necessary to implement the selection and activation of menu options using a definitive approach will be described later. The role of the Scout definitions is to present the values of the variables of interest to the user in a comprehensible way.
T5.2.2. Modelling a Screen Layout Using Scout
When the term 'modelling' is used, we mean that we have already at least a mental picture, if not anything more concrete, of what the target looks like. There is a distinction between modelling activity and exploratory design. For example, in the case of screen layout, exploratory design is necessary when the final screen layout is not known. Bits and pieces may be added, deleted or modified from the intermediate implementations until the designer is satisfied. For the Jugs problem, the emphasis is on modelling rather than exploratory design since the screen layout is prescribed rather than designed from scratch. We are basically following the layout of the output from the original Jugs program by Townsend. Therefore, before we do any exploration on the screen layout design, we begin by modelling the original Jugs output using Scout.
In the following sub-sections we will first discuss the process of modelling a screen layout using Scout, then consider some advantages of definitive notation in the light of the modelling technique demonstrated by Scout.
After the screen layout is modelled in Scout, the designer may go on exploring the design. The advantages of Scout, and in general definitive notation, towards exploratory development of software are going to be discussed in section T1.4.
T5.2.2.1. Screen Layout Modelling Process
There are three informal stages for developing a Scout description of a screen layout:
1. Develop an idea of what the screen display should look like. For example, Figure 5.1 is what the screen should display when the Jugs program is first started. The colour of the menus represents their availability - black on white indicates a valid option.
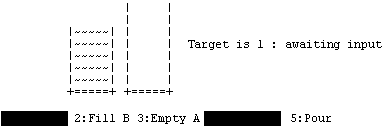
Figure 5.1: A Sample Jugs Output
2. Characterise the screen layout by identifying the common relationships in the screen layout. Figure 5.2 shows the design for the geometrical information of the Jugs output. Other characteristics such as the number of tildes required to fill up to the level contA (which is widthA * contA) can be identified as well.
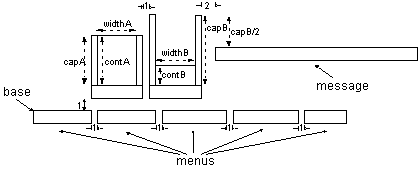
Figure 5.2: Screen Layout Design
3. The programming task is almost finished although we have not actually
written down anything in the Scout notation! To finish off the work, this
final step transforms the information obtained from the first two steps
into the Scout notation. Listing 5.1 and Listing 5.2 show parts of the
Jugs game screen layout in the Scout notation. The complete Jugs example
(Scout definitions for the screen layout and EDEN definitions for other
part of the program) can be found at [jugsBeynon2002].
point base = {1.c, n.r} |
|
This method of developing a screen layout is similar to writing a program in a traditional software development process; the first two steps are analogous to obtaining an (informal) specification whereas the last step is analogous to implementing the specification. Although the theme of this thesis is exploratory software development, the discussion in this section is not unrelated. The simplicity of the modelling method indicates how easily we can relate a definitive script to reality. This certainly helps the exploratory software designer to understand and make changes to the current design.
T5.2.2.2. Special-Purpose Notation for Specific Task
The purpose of screen layout design is to decide where information should be placed and how it should be presented. The Scout notation restricts the areas allocated for displaying information to be rectangular or a group of rectangles. For this reason, the Scout notation permits only simple layout design. However, the design of the notation has already taken into account some assumptions of the characteristics of the display unit and the usual layout designs. For example:
The addressable points on a display unit normally form a grid. Moreover, Scout is only a notation for describing screen layout and is not a general graphics display notation. Therefore, the obvious choice of the Scout coordinate system is the Cartesian Coordinate System.
ii) Area Allocation
A window in Scout means a fixed region in which a piece of information is displayed. The region that can be allocated depends on the type of information to be displayed. Although no 2-D line drawing window appears in the Jugs example, Scout, at its present stage of development, can incorporate DoNaLD graphics, ARCA diagrams and text. If graphics is going to be displayed, the region must be a box. The following fields are significant in the definition of the window:
| type: DONALD (or ARCA)
box: b pict: picture-name |
| type: TEXT
frame: f string: s |
iii) Presentation of Information
Again, what can be controlled depends on the type of information being presented. We can, for examples, shift and scale the image of the DoNaLD pictures and change the background colour of the window and the colour of the lines. For text, we can change its alignment, foreground and background colour.
iv) Combining Windows
In some cases, say a windowing system, windows may overlap. The Scout notation defines a display to be an ordered list of windows such that if there is overlapping, one window overlays another if it precedes the other in the list (cf. Listing 5.2). This presumes that it is never necessary to represent a situation such as Figure 5.3 where windows overlay cyclically.
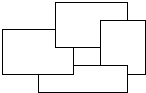
Figure 5.3: Cyclic Overlapping Windows
Although the Scout notation looks simple, its design has already involved a lot of assumptions about the nature of the physical displays, the types of application and the ways of denoting and manipulating information. For this reason, expressing the screen layout in Scout (step 3) is straightforward. Other definitive notations are also special-purpose notations. This means that the notations, including the data types and operators, are designed for particular application domains. This helps to give definitive notations high expressive power.
Moreover, using special-purpose notations reduces the learning time
and the programming time of the programmer, increases the understandability
and hence eases the maintenance of the program.
Modelling involves analysis and representation of a real world system.
Persistent relationships between objects and interaction between objects
are two kinds of behaviour we may often observe. For instance, consider
the following scenario. “A table lamp lights up when the switch
is at position ON and it turns off otherwise - this is an persistent relationship.
There is interaction between a man and the light switch so as to change
the state of the switch. This interaction does not change the persistent
relationship between the brightness of the table lamp and the light switch,
but some interactions do. A sudden impact on the table lamp may cause breakage
of the filament so that the relationship is changed to - the table lamp
will not glow irrespective of the position of the light switch. This shows
that a persistent relationship is not necessarily permanent; it is subject
to change by interaction.
We have already experienced problems, such as verification and concurrency, with imperative programming which disregards the persistent relationships; we have also the experience of using functional programming which stresses the permanency of persistent relationships - making use of higher-order function to prevent change of relations adds a degree of complexity to the relationships. Definitive programming paradigm enables us to describe persistent relationships without ruling out the possibility of relationship changes by interaction. Hence it is desirable for modelling.
Furthermore, a set of definitions shows not only the design of the model of current state, it also provides hints for change of design. The intelligent use of constants and formulae in defining variables indicates the flexibility of the model. Using the Jugs example as an illustration, the point base is defined in Figure 5.1 to be {1.c, n.r} where n is currently defined as 20. Redefining base as {1.c, 20.r} rather than {1.c, n.r} does not affect the value of the point base and hence the whole picture remains unchanged. But the definition
base = {1.c, n.r}
gives base a degree of freedom - the point base can be moved vertically without changing its definition but only changing the explicit value of n. Of course there is no rule to guarantee that the definition of base is fixed or that the definition of n is going to be altered, but the use of implicit formulae and explicit values in definitions suggests that the variables defined by explicit values are more liable to change and the variables defined by implicit formulae are more persistent.
Therefore, variables in a definitive notation are more than variables
containing pure values; the formulae defining the variables are significant.
In fact, they are more significant than the values. This is because the
variables must specify a unique set of values if sufficient definitions
are given, but if some definitions are missing (i.e. the model is incomplete)
the formulae define latent values of the variables.
Since definitive notations are special purpose notations, a script
written in a single definitive notation is generally insufficient for specifying
the whole application. On the other hand, the usefulness of definitive
notations is not undermined by this; a script can still be used to model
a particular aspect, such as the screen layout, of the application.
With reference to the Jugs example, the Scout definitions only describe the screen layout. They do not specify how the variables like contA and valid1 are maintained. In fact the control in the Jugs example is written in EDEN, a general purpose definitive language. A way of integrating definitive notations via EDEN will be discussed in the next chapter. The basic idea is to translate different kinds of definitions into a single definitive language so that variables of different definitive notations can communicate via definitions. This means, for example, that in order to animate the Jugs layout, designed in Scout, it is only necessary to append the EDEN script and a set of actions that defines the Jugs control. Therefore, a definitive paradigm for representation of state provides a neat way of separating control and presentation. The advantages of the separation are:
The development of the control can be made independent of the development of the presentation; this leads to faster program development and aids the division of labour. Different views of the same application are possible at the same time. For instance in the Jugs example, we can execute the Scout display specification together with the display specification, suitable for a tty display, that is incorporated in the original EDEN Jugs control (cf [jugsBeynon1988]). As a result, another Jugs display will appear on a tty terminal.
The screen layout target is not always known at an early stage of screen layout design. A practical way of screen layout design is to obtain a first approximation and then gradually evolve the design through prototyping and experimentation. During an exploration of design, one of the following activities may be performed:
2. Displaying new items
3. Relocating the display items
4. Modifying relationships between variables
5. Testing of design - changing the parameters or testing data
T5.2.3.1. Convenient State Changes
Although redefining a variable may cause changes to the values of many variables and hence the screen display, the only difference the redefinition makes to the definitive state is the definition of that particular variable. Therefore, reversing the changes made by the redefinition only requires restoring the original definition of the variable. Timbleby argues that the user of an interactive system must be able to undo errors. With a good undo available, users will be encouraged to experiment with the system. In our current system, no undo facility has been implemented. It is our intention to leave the system in a raw operational mode so that there is no fancy user interface to distract our attention from developing higher level control for transitions of definitive states. However, the simplicity of undoing the effect of a definition is an advantage of definitive notations for exploratory design.
T5.2.3.2. Flexible Definition Arrangement
Changing the two pour menu options to one pour option in the jugs example
involves replacing of the definition:
|
|
|
|
with the addition of the following definitions:
window pourwindow = { |
Listing 5.3 defines all the necessary information required to display what can be seen on the screen as the 'Pour' menu option (i.e. the region, content and attributes of the window are all defined). The only piece of missing information is menu4box, which is part of the display information of another menu option. Listing 5.3 is therefore similar to a window object in object-oriented programming terms, except that in our paradigm no information hiding is assumed. This grouping of definitions here and the grouping of definitions illustrated in Listing 5.1 and 5.2 shows two grouping methods with different emphasis. One groups the definitions relating a visible window whilst the other groups the definitions according to their functionality. Flexibility of definition arrangement is possible because the ordering of definitions in a script is insignificant. The advantages of having this flexibility are:
2. Regrouping of definitions will not affect the meaning of the script.
It is possible therefore to develop tools to rearrange definitions in ways
that can assist our understanding of the script. Particularly useful arrangements
might be obtained by sorting the definitions by types or by their dependency
hierarchy.
[BY89] Definitive Interfaces as a Visualisation Mechanism
[BNRSYY89] Software Construction using Definitions CS RR#147