Figure 1: A Way of Partitioning a Non-rectangular Region
T5.1. The Design of Scout
A preliminary design for the Scout notation was described in Simon Yung's final year undergraduate project report [Yung88]. In its original form, Scout was designed for laying out text; it was subsequently enhanced to interface with DoNaLD (and with ARCA, though this is beyond the scope of this course). The following lecture notes are due to Simon Yung; they give a good insight into issues for the design of a definitive notation.
The choice of the Scout notation primitives is based on the assumed nature of the screen and the manner in which it will be used in particular applications. For instance, a newspaper layout may require multi-column format, whilst rectangular boxes suffice for a typical window-based application. For these tasks, high resolution graphical display is a reasonable assumption. Provision for colour display is also preferred.
Complicated drawings are assumed to be handled by other definitive notations. In fact, the purpose of designing different definitive notations is to ensure that different kinds of application can be addressed in appropriate notations. DoNaLD, CADNO and ARCA are some definitive notations designed for describing different kinds of graphics. Other definitive notations for describing graphics are also conceivable. It is not our intention and it is not appropriate to use Scout to describe every single detail of what the screen will display. Scout, therefore, does not provide a set of drawing primitives but is intended to deal with simpler tasks such as screen layout, scaling and other operations at the pixel level. Scout's special role is to specify where and how these images described by other definitive notations are displayed. In principle, the role of Scout should be confined to coordinating the use of different definitive notations to form a display, but because there is no definitive notation for displaying text so far and text is almost indispensable in any serious application, a part of the Scout notation is concerned with the display of text strings. However, it is intended to develop other definitive notations to deal with more complicated text displaying tasks such as those encountered in desktop publishing or word processing applications.
T5.1.1. The Window Data Type
Layout design in Scout is based on the answers to the following three
questions: What are the things to be displayed? Where are they to be displayed?
And how are they to be displayed? This natually leads to the concept of
the Scout window data type. The type window is a union of subtypes: one
subtype is designed for each definitive notation. Each subtype has a number
of fields. The number of fields and the types of the fields may vary depending
on which notation this subtype refers to. Generally speaking, a window
should have fields that define
2) what information (e.g. which DoNaLD picture or which text string) is to be displayed;
3) the region of the screen onto which the required information is mapped;
4) the supplementary information that that definitive notation needs.
| Text Window | ||
| field name | type | description |
| type | content | Must be the value TEXT |
| string | string | The string to be displayed |
| frame | frame | The region in which the string is shown |
| border | integer | Width of the border of the boxes of the frame |
| alignment | just | NOADJ, LEFT,RIGHT, EXPANDand CENTRE are the possible values to denote no alignment, left justification, right justification, left and right justification and centre of the text inside each box in the frame |
| bgcolour | string | Colour name for the background colour of the text |
| fgcolour | string | Colour name for the (foreground) colour of the text |
where point = integer X integer
box = point X point
frame = list of box
| DoNaLD Window | ||
| field name | type | description |
| type | content | Must be the value DONALD |
| box | box | The region in which the DoNaLD picture is shown |
| border | integer | Set the border width of the bounding box |
| pict | string | The name of the DoNaLD picture |
| xmin | point | |
| ymin | point | Show the portion of the DoNaLD picture |
| xmax | point | bounded by the points (xmin, ymin) and (xmax, ymax) |
| ymax | point | |
Comments on the window data types:
2) There is no formal restriction on how to define a region. Nevertheless, the choice of method should be governed by the nature of application. The three available subtypes have already employed two ways of defining regions. In a DoNaLD or ARCA window, a region is defined by a box, whereas in a text window, a region is defined by a list of boxes. A single box is good enough to frame one picture but a list of boxes is required if a long passage of text is to be displayed in multiple columns.
3) Notice that there are almost no fields in common between the graphics window subtypes and the text window subtype, so the type window may be better understood by the abstract formula
A display is a collection of windows. Because the windows may overlap, there is a partial ordering among the windows. For simplicity, a display is defined to be a list (total ordering) of windows.
In general, a display variable represents a conceptual screen; only the distinguished display variable screen denotes the physical screen. There are simple rules for mapping the variable screen onto the physical screen:
2) the x-coordinate counts from the origin to the right, one unit per pixel;
3) the y-coordinate counts from the origin to the bottom, one unit per
pixel.
Because there is a great flexibility in the design of the window data type, the set of data types and operators in Scout may be extended in the future. There are, however, some essential data types in Scout: integer, point, window and display. Associated with them are basic operators for integer arithmetic, vector manipulation, list manipulations, construction and selection. The following table shows the basic Scout operators and functions for the four essential data types.
Operators: +, -, *, /, % (remainder), - (unary minus)
Meaning: Normal integer arithmetic
Example: 10 % 3 gives 1
Constructor: {x, y}
Meaning: Construct a point
Example: {10, 20} is a point with x-coordinate 10 and y-coordinate 20
Operators: +, -
Meaning: Vector sum and vector subtraction
Example: {10, 20} - {20, 5} gives {-10, 15}
Selector: .1, .2
Meaning: Return the 1st (x-) coordinate and 2nd (y-) coordinate resp.
Example: {10, 20}.1 gives 10
Constructor:
{field-name: formula, field-name: formula, ..., field-name: formula}
Meaning: Constructing a window
Example: { type: DONALD, box: b, pict: "figure1" }
Selector: .field-name
Meaning: Return the value of the field
Example: { type: DONALD, box: b, pict: "figure1" }.box gives b
Constructor: < W1 / W2 / ... / >
Meaning: Construct a display; if W1 and W2 overlap, W1 overlays W2
Example: < don1 / don2 >
List fn: insert(L, pos, exp)
Meaning: Return L with the expression exp inserted in position pos
Example: insert(<w1, w2, w3>, 2, new) gives <w1, new, w2, w3>
List fn: delete(L, pos)
Meaning: Return L with the posth element deleted
Example: delete(<w1, w2, w3>, 2) gives <w1, w3>
Operator: if cond then exp1 else exp2 endif
Meaning: if cond gives non-zero value (true) then returns exp1 else returns exp2, here, exp1 and exp2 must have the same type.
Example: delete(<w1, w2, w3>, 2) gives <w1, w3>
As mentioned, text layout should ideally be described by another definitive notation. Since no such notation exists, the Scout notation is designed to handle simple text layout. To this end, Scout incorporates a text window subtype. This text window subtype differs from other window subtypes in that its content is a string defined within Scout rather than a virtual screen prescribed outside Scout by another definitive notation. As a result, string becomes one of the Scout data types.
Associated with the string data type is a set of operators useful for displaying a text string. String concatenation (//), string length function (strlen), sub-string function (substr) and integer-to-string conversion (itos) are the basic Scout string manipulation functions. There are two postfix operators -.r and .c - which are specially designed. Since the basic geometric unit in Scout is the pixel but the size of a block of text is more conveniently specified as "number of rows by number of columns", it is convenient to introduce functions returning the row height and the column width in pixels. .r is the function meaning "multiply by the row height" and .c is the function meaning "multiply by the column width". These functions are appropriately represented by postfix operators because they work very much like units. For example, {10.c, 3.r} refers to a point 3 rows down and 10 columns right to the origin. A similar consideration influences the design of a box, a data type for defining regions. The region associated with a box is sufficiently defined by its top-left corner and its bottom-right corner, and this is a convenient method of definition in the case of graphics. For a block of text, however, the bounding box is more conveniently defined by specifying the top-left corner and the dimensions of the box in terms of number of rows and columns. For instance, [{0, 0}, 3, 10] refers to a box with the origin as its top-left corner which is suitable for displaying three rows by ten columns of text. More examples of this kind can be found in the Jugs example (see e.g. jugsPavelin2002).
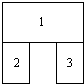
Because displaying a string is different from displaying an image, the way of specifying a region for displaying text is different from that for displaying an image. Our solution is to divide an arbitrary shape into subregions, each of which is a box. The definition of a region will then be a ordered list of boxes. For example, the region shown below is interpreted so that a string should be filled in the boxes in the order 1, then 2, then 3.

Figure 1: A Way of Partitioning a Non-rectangular Region
This "frame = list of boxes" definition of region is not perfect. For instance, if two boxes overlap (which may depict the overlapping of two sheets of the same document), which box should be put on top is still ambiguous. However, except for serious desktop publishing, this definition of region should be adequate for most applications.