The De Young Keizer model

One of the more popular of the standard models underlying Ca2+ oscillations between the ER and the cytosol is the biophysical De Young Keizer (DYK) model based around a detailed description of the dynamics for IP3 receptors (IP3Rs). It is believed to be the first model that explains oscillations on the basis of only the IP3R/channel and a single Ca2+ pool. The DYK model mimics the molecular subunit configuration of the IP3R to reflect the activation/inactivation sequence of the channel that results from the binding of Ca2+ and IP3 to the IP3R. 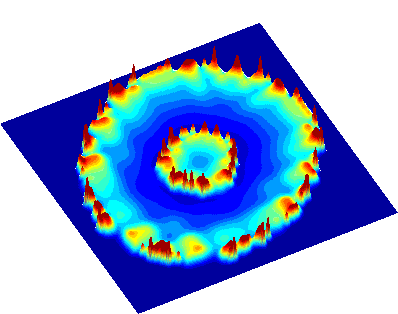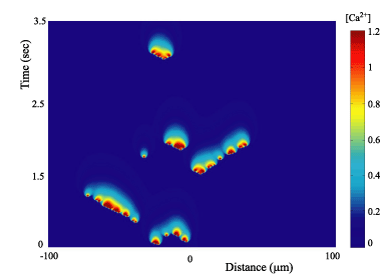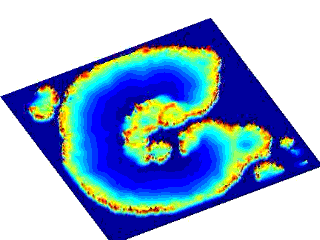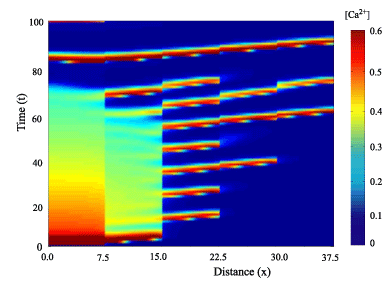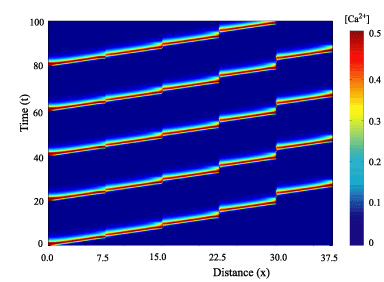For the most recent set of experimentally determined parameter values the DYK model supports an interesting form of bifurcation structure including global bifurcations. A variety of propagating patterns are sustained by this model including travelling pulses and periodic travelling waves, 2n- periodic orbits and 2n-homoclinic orbits. Moreover, using a kinematic theory of irregular wave propagation it is possible to predict the existence of a non-periodic travelling wave (that connects two periodic wave trains).

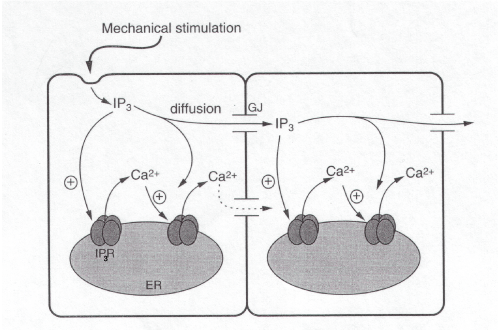
Essential fluxes involved in intracellular Ca2+ oscillations Calcium is removed from the cytosol in two principal ways: it is pumped out of a cell and is sequestered into ER/SR. Calcium influx also occurs via two principal pathways: inflow from the extracellular medium through Ca2+ channels in the surface membrane and release from internal stores.

The Fire-Diffuse-Fire type model

One dimension

The Fire-Diffuse -Fire model of Pearson et al. provides an idealised model of Ca2+ release within living cells using a threshold process to mimic the nonlinear properties of Ca2+ channels. This model was originally intended as a model of cardiac myocytes in which calcium release occurs via RyR Ca2+ channels located in a regular array in the SR. However, one of the major successes of the FDF model is that it can be mathematically analysed both in the discrete and continuous limits. Much of the travelling wave behaviour of the biophysical DYK model (in particular solitary and periodic waves) can be reproduced by the generalised version of the FDF model under parameter variation.	Schematic representation of the FDF model
Example of two lurching pulses	Saltatory travelling wave in the discrete FDF model
Making the assumption that release events occur on a regular temporal lattice the FDF model is simplified so that it may be re-written in the language of binary release events. When considering a discrete set of release sites and calcium puffs or sparks that have a simple on/off temporal structure the calcium profile can be solved for in closed form. A dynamics for the release events are calculated via a thresholding of the calcium profile at a release site. This computationally cheap version of the FDF model provides an accurate representation of the original model. It is both natural and straightforward to generalise our one dimensional FDF threshold model to two dimensions. Varying system parameters reveals that the model supports many patterns of wave propagation behaviour including regular and irregular lurching travelling pulses, colliding and periodic waves, travelling fronts and spiral waves as well as abortive waves.	Periodic travelling wave with irregular spaced release sites

Two dimensions

Animation of the FDF model on the regular square lattice

Animation of the FDF model on the irregular square lattice

Initiation of a spiral wave on the irregular square lattice

Stochastic Fire-Diffuse-Fire model

One dimension

An integrative multi-scale FDF framework opens up new possibilities for mathematical progress in studying the dynamics of Ca2+ release in cells. We generalise the FDF threshold model to incorporate stochastic effects. The stochastic nature of release is incorporated via the introduction of a simple probabilistic rule for the release of calcium from internal stores. This is a natural way to investigate puff/spark to wave transitions within a spatially extended cell model with a discrete distribution of release sites. Numerical simulations demonstrate a variety of noise-sustained patterns of wave propagation. In the parameter regime where deterministic waves exist, it is possible to identify a critical level of noise defining a non-equilibrium phase-transition between propagating and abortive structures. This transition is the same as for models in the directed percolation universality class.

Stochastic travelling wave

Two dimensions

Animation of the stochastic FDF model (noisy circular and spiral waves)

Array enhanced coherence resonance in the stochastic FDF model

Intercellular Ca²⁺ waves

In many cell types, an initiated wave of increased intracellular Ca2+ can spread from cell to cell to form an intercellular wave. Mechanical stimulation of a single cell initiates the production of IP3 in that cell and consequent release of Ca2+. Some of this IP3 moves through gap junctions to neighbouring cells, releasing Ca2+ from internal stores there. A small amount of IP3 can stimulate a large release of Ca2+ via a positive-feedback process. The subsequent transport of Ca2+ through neighbouring cells stimulates further release resulting in an intercellular Ca2+ wave. This hypothesis for the propagation of intercellular Ca2+ waves relies on the passive diffusion of IP3 between cells via gap junctions.

Propagation of intercellular Ca2+ waves through gap junctions

Intercellular Ca2+ waves in the DYK model witn mobile IP3

Intercellular Ca2+ waves in the FDF model with mobile IP3